Spurpunkte mit Koordinatenform ausrechnen

Für
$ax+by+cz=d$

Um den Spurpunkt mit der $x_1$-Achse zu berrechnen
$S_1(x|0|0)$
$ax+0y+0z=d$
$ax=d$

$x$ ausrechnen
Spurpunkt: $S_1=(x|0|0)$

Alternative

$E:x_1-2x_2+2x_3=8|:8$
$E:\frac{x_1}{\mathbf{8}}\mathbf{-}\frac{x_2}{\mathbf{4}}+\frac{x_3}{\mathbf{4}}=1$

Eine Ebene mit der Koordinatenform $\frac{x_1}{a_1}+\frac{x_2}{a_2}+\frac{x_3}{a_3}=1$ und $a_{1,2,3}\ne 0$ hat die Spurpunkte $S_1(a|0|0),S_2(0|a_2|0),S_3(0|0|a_3)$.

Aufgaben

1b)

$E:x_1-2x_2+2x_3=8$

$S_1$:
$x_1=8$
$S_1(8|0|0)$

$S_2$:
$-2x_2=8$
$x^2=-4$
$S_2(0|4|0)$

$S_3$:
$2x_3=8$
$x_3=4$
$S_3(0|0|3)$

Achsenabschnittsform einer Ebene

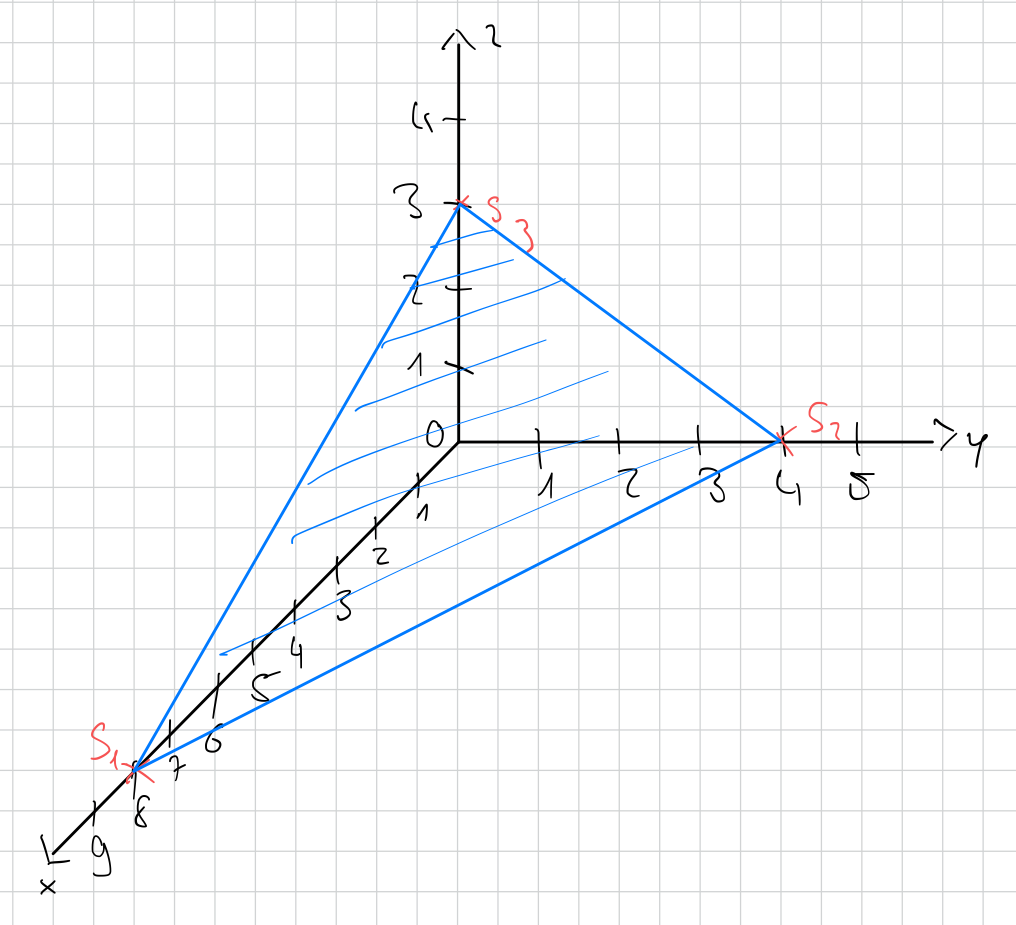
Eine Ebene in Koordinatenform $E:a\ast x_1+b\ast x_2+c\ast x_3=d$ kann "einfach" in die Achsenabschnittsform (durch Division) überführt werden.

Die Achsenabschnittsform lautet:

Eine solche Ebene hat die Spurpunkte
$S_1(a_1|0|0)$
$S_2(0|a_2|0)$
$S_3(0|0|a_3)$

5a)

$\frac{x_2}{3}+\frac{x_3}{4}=1|\ast 12$
$4x_2+3x_3=12$

b)

$\frac{x_1}{1}+\frac{x_2}{3}=1|\ast 3$
$3x_1+x_2=3$

c)

$\frac{x_1}{3}=1|\ast 3$
$x_1=3$

d)

$\frac{x_1}{2}+\frac{x_3}{4}=1|\ast 4$
$2x_1+x_3=4$

6a)

1

Spurpunkte:
$E:5x_1+6x_3-30=0$
$5x_1+6x_3=30|:30$
$\frac{x_1}{\frac{1}{6}}+\frac{x_3}{\frac{1}{5}}=1$

$S_1(\frac{1}{6}|0|0)$
$S_3(0|0|\frac{1}{5})$

Spurgeraden:
$s:\overrightarrow{x}=\left(\begin{array}{c}\frac{1}{6}\\ 0\\ 0\end{array}\right)+u\ast \left(\begin{array}{c}-\frac{1}{6}\\ 0\\ \frac{1}{5}\end{array}\right)$

2

Spurpunkte:
$E:x_1-6x_2=6|:6$
$\frac{x_1}{\frac{1}{6}}+\frac{x_2}{-1}=1$

$S_1(\frac{1}{6}|0|0)$
$S_2(0|-1|0)$

Spurgeraden:
$s:\overrightarrow{x}=\left(\begin{array}{c}\frac{1}{6}\\ 0\\ 0\end{array}\right)+u\ast \left(\begin{array}{c}-\frac{1}{6}\\ -1\\ 0\end{array}\right)$

3

Spurpunkte:
$E_3:4x_3-20=0$
$4x_3=20|:20$
$\frac{x_3}{5}=1$

$S_3(0|0|5)$

Spurgeraden:
$s:\overrightarrow{x}=\left(\begin{array}{c}0\\ 0\\ 5\end{array}\right)+u\ast \left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)$